* 개인적으로 독학한거라 최적화 알고리즘이 아닐 수 있습니다.
* 아래보다 더 쉬운 알고리즘도 있지만 개인적인 생각으로 상황에 따라 벽을 길게 돌아갈 것 같아서 안씀.
0. 오픈리스트라는 리스트(배열)를 만든다. 그리고 전체 맵 좌표가 담긴 리스트가 필요하다. 맵좌표의 리스트들은 갈수있는 길인지, 가중치, 최단거리, 합, 리스트 상태 확인변수 이렇게 하위 리스트들을 갖는다.
1. 시작지점 주위 8개의 타일중 갈 수 있는길(벽, 장애물 아닌 길)을 오픈리스트에 넣는다. 그리고 해당좌표에 오픈리스트라는 표시를 해둔다.
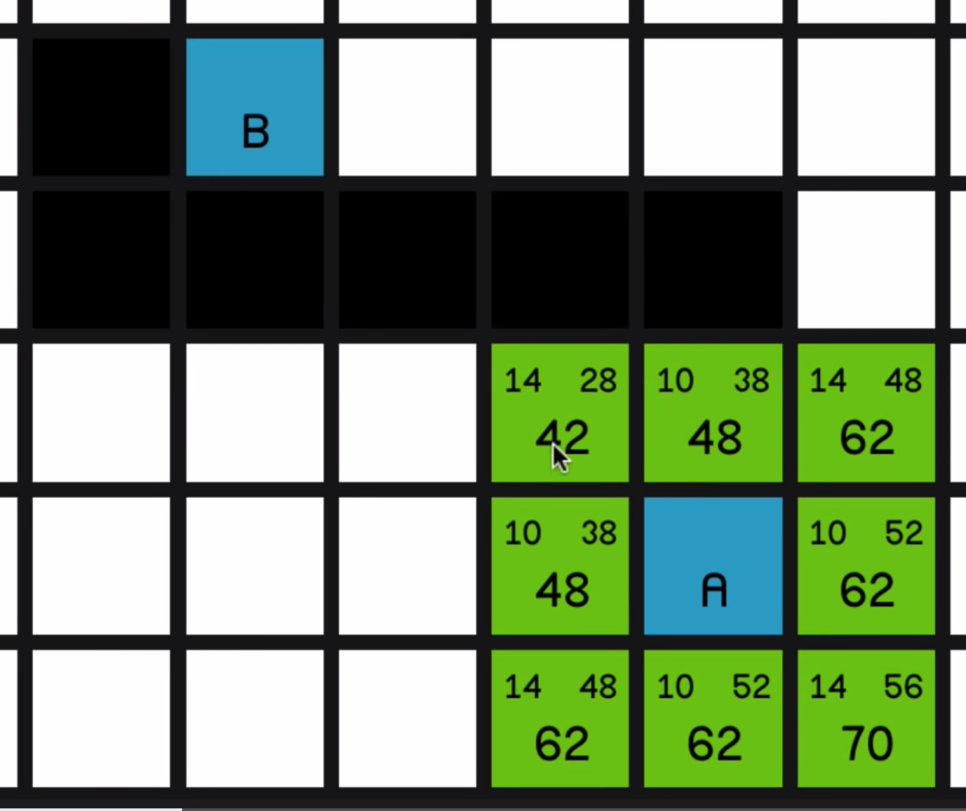
1.1. 각 타일에 가중치, 최단거리, 둘의 합을 넣어둔다.
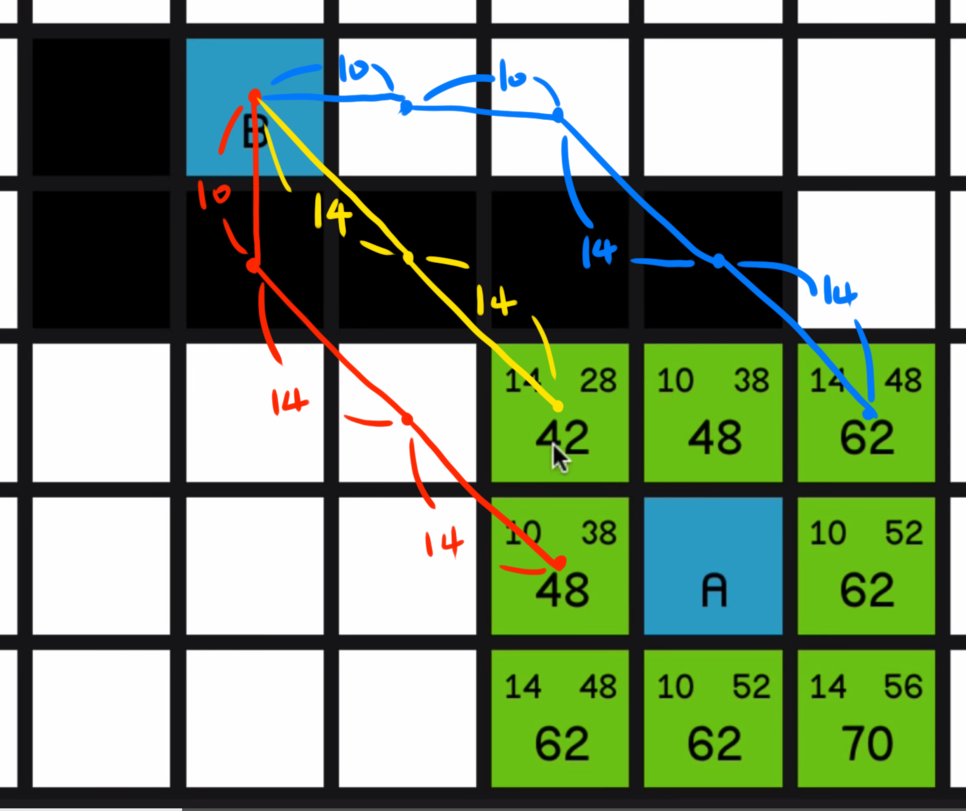
1.2. 가중치는 피타고라스의 정리를 통해 구하면 되는데 수평, 수직으로 이동할 때는

이므로 10을 적용 대각선은

이므로 루트2 인 1.4에 10을 곱하여 14를 적용.
1.3. 최단거리는 해당지점과 도착지점의 사이의 대각선을 포함한 최단거리를 구해야 된다.
해당지점 좌표와 목표지점의 좌표를 서로 뺀다.

서로 뺀 값 x, y 중에서 작은 값은 14를 적용 더 큰 값은 작은값을 빼고 10을 적용시킨다.
x가 더 작은 값이라면 ( x * 14 + { y - x } * 10 ) 이렇게 해준다.
2. 오픈리스트에서 수치가 가장 작은 것을 찾아내어 해당 좌표에 클로즈 리스트라고 표시해 둔다.
클로즈 리스트는 최단길을 찾을때 쓰인다.

2.1. 클로즈 리스트 라고 표시를 해둔다음 주변 8개의 좌표들의 가중치(현재기준 좌표의 가중치를 추가로 더한다), 최단거리, 합을 구한다.
2.2. 오픈리스트에 안들어 있는게 있으면 오픈리스트에 넣고 오픈리스트에 이미 있다면 이전값(가중치 최단거리의 합)과 비교하여 더 작은것을 적용한다.
3. 2번을 계속 반복한다. 그리고 주위 8개 중에 도착지점이 있다면 반복을 멈춘다.
4. 이제 최단거리를 구해야 하는데 최단거리는 도착지점에서 시작지점으로 찾아나가면 된다. 그리고 최단길을 넣을 베스트 리스트를 만든다.
4.1. 도착지점이에서 시작하여 주위 8개의 타일을 조사한다. 8개중에 클로즈리스트가 있다면 베스트 리스트에 넣는다. 주위에 클로즈 리스트가 여러개라면 젤 작은걸 넣는다. 그리고 해당 좌표를 베스트 리스트라고 표시한다.
4.2. 베스트 리스트라고 표시한 지점 주위 8개에서 또 제일 작은 클로즈 리스트를 찾는다.
4.3. 시작지점에 닿을때 까지 계속 반복한다.
4.4. 시작지점에 닿으면 최단길 찾기 끝
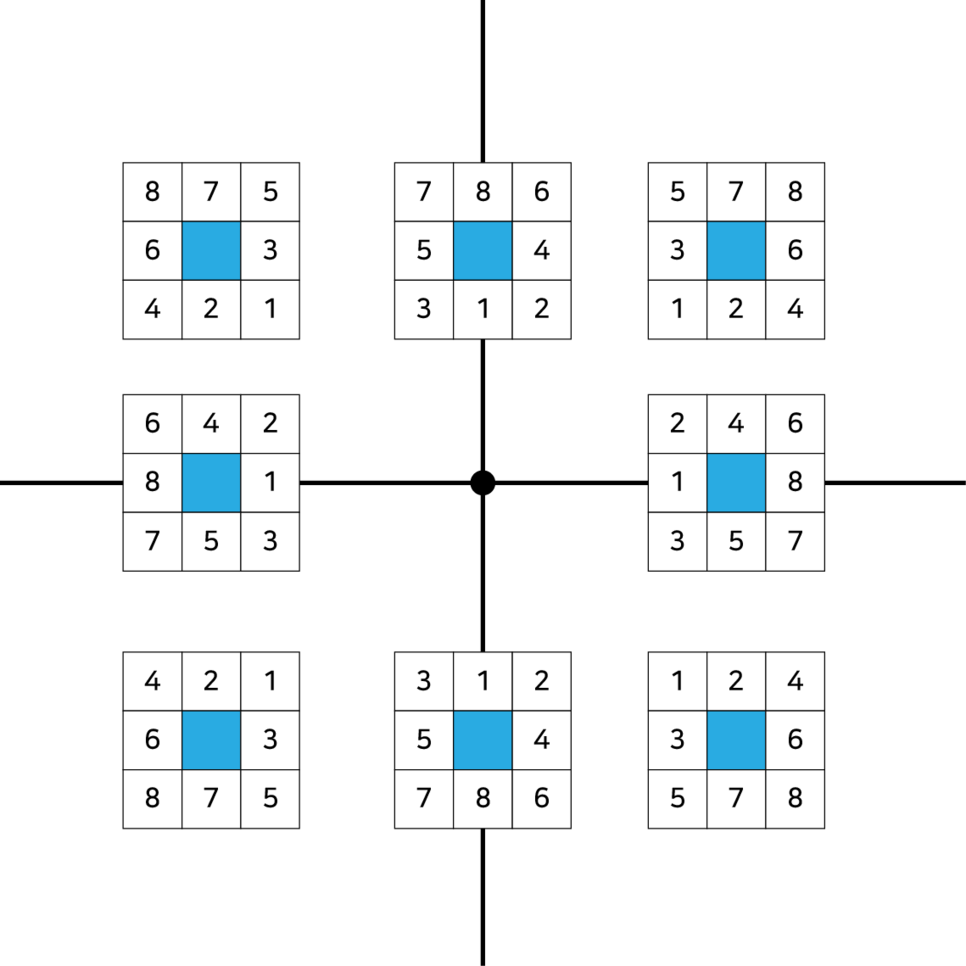
5. 만약 최단 길이 삐뚤삐뚤 하다면 최단길을 찾을 때 기준지점과 시작지점의 위치를 비교하여 위치에 왼쪽에 있다면 오른쪽의 좌표를 먼저 조사한다던지의 처리를 해주면 된다. 값이 같은 클로즈 리스트가 있을수도 있기 때문.
가장 좋은 방법은 에셋을 사서 쓰는 방법이다.
참고
'기타 정보' 카테고리의 다른 글
| (0,0) 기준 좌표 위치에 따른 범위 (0) | 2020.11.23 |
|---|
